平方损失

平方损失 Square Error ，作为机器学习中最为经典，也是最为朴素的损失算法，值得进一步进行探讨。

本篇文章对背后的数学原理、最优化算法进行探讨。

概率数学原理

简单理解（图像）

数据如下表

$x_0$	$y$
1	1
2	3
3	2
4	6
5.06	7.23
6	7

上图中的绿色点都是对应数据样本在二维笛卡尔坐标系中的描点。

现在需要考虑的是如何衡量数据样本与预测值的偏差。

在几何中可以通过距离表示，那么我们只需要计算距离即可。

由平面直角坐标系距离公式可知

$L^2=(x_1-x_2)^2+(y_1-y_2)^2$

代入数据点$(x_0,y)$，预测点$(x_0,h(x_0))$可得

$\begin{aligned} L^2 &= (x_0-x_0)^2+(y-h(x_0))^2\\ &= (y-h(x_0))^2 \end{aligned}$

即可导出均方误差公式为

$E(x^i)=\frac{1}{2m}\sum_{i=0}^m(y^i-\theta x^i)^2$

深入理解（概率统计）

机器学习中的很多算法并不只是表面的直观理解，其实内部还有很多的数学原理。

这部分通过极大似然法来对为什么是平方来进行理解。

对于真实世界的预测，我们可以写为

$y=\theta x + \varepsilon$

我们令 $\varepsilon$ 为真实世界中被忽视或无法获取的特征的和，可以变形为

$\varepsilon=y - \theta x$

在生活经验中，$\varepsilon$ 非常接近钟形分布，即高斯正态分布，于是

$\varepsilon \backsim N(\mu,\sigma^2)$

展开得

$f(\varepsilon)=\frac{1}{\sqrt{2\pi}\sigma}\cdot e^{-\frac{(y-\theta x-\mu)^2}{2\sigma^2}}$

我们计算出出现 $f(\varepsilon)$ 的概率，记为 $P(\varepsilon)$

$\begin{aligned} P(\varepsilon) &=\prod_{D}{f(\varepsilon)}\\ &=\prod_{D}{\frac{1}{\sqrt{2\pi}\sigma}\cdot e^{-\frac{(y-\theta x-\mu)^2}{2\sigma^2}}} \end{aligned}$

我们选择对它取对数操作，对数是增函数

$\begin{aligned} L(\varepsilon) &= \ln P(\varepsilon)\\ &=\sum_{D}\ln\frac{1}{\sqrt{2\pi}\sigma}+\sum_{D}\ln e^{-\frac{(y-\theta x-\mu)^2}{2\sigma^2}}\\ &=\sum_{D}\ln\frac{1}{\sqrt{2\pi}\sigma}+\sum_{D}{-\frac{(y-\theta x-\mu)^2}{2\sigma^2}} \end{aligned}$

因为第一项是一个常数，所以我们要让 $P(\varepsilon)$ 最大，于是要让 $L(\varepsilon)$ 最大，于是要让下式最小

$\frac{(y-\theta x-\mu)^2}{2\sigma^2}$

只需要不断优化 $\theta$ 使得 $(y-\theta x)^2$ 最小，即

$\text{minimize} \ {(y-\theta x)^2}$

这意味着接下来我们需要通过不同方法进行上述操作

梯度下降

定义

梯度下降法 (gradient descent) 是一个最优化算法，常用于机器学习和人工智能当中递归逼近最小偏差模型。

在已知表达式的情况下可以代替二分三分，且效率较高。

在发展过程中衍生出了随机梯度下降算法和批量梯度下降算法，本文介绍批量梯度下降算法。

数学原理

推导过程

以线性回归为例，不妨令 $x^i$ 为第 $i$ 组输入数据，$h(x^i)$ 为预测结果

$h(x^{(i)})=\theta x^{(i)}$

(损失函数)

此处使用均方误差（又称最小二乘法）

令误差函数为$E(x^i,y^i)$得

$\begin{aligned} E(x^i,y^i) & =\frac{1}{2m}\sum_{i=0}^m (y^i-h(x^i))^2\\ & =\frac{1}{2m}\sum_{i=0}^m(y^i-\theta x^i)^2\\ \end{aligned}$

由于我们的目的是通过数据拟合出函数，换句话说是调整 $\theta$ 的值

所以我们更换主元为 $\theta$ ，并构造损失函数 $J(\theta)$ 得

$\begin{aligned} J(\theta) & =\frac{1}{2m}\sum_{i=0}^m(y^i-\theta x^i)^2\\ \end{aligned}$

(批量梯度下降)

并对上式求关于 $\theta$ 的偏导得

$\begin{aligned} J'(\theta)= \frac{\partial J(\theta)}{\partial \theta_j} & = \frac{1}{m}\sum_{i=0}^m(\theta x^i-y^i)x_j^i \end{aligned}$

我们需要通过上式确定迭代的方向，并不断迭代直到收敛

于是得到递推式为

$\theta_j=\theta_j-J'(\theta_j)\alpha$

上式中的$\alpha$为学习率，可以控制没移动一步的快慢。若$\alpha$设置过大，则可能出现偏差越迭代越大的情况；若$\alpha$设置过小，则训练耗时越大。需要正确选择学习率的大小。

迭代的过程如下图所示.

过程详解

可以用盲人爬山来简单形容。
盲人爬山闭着眼，要用脚试一下是往下的，那就走，一直这样操作，最终下山。当然这也就暴露出了其问题，无法一次性找到全局最优解。

可以用图像来简单说明。

这是损失函数（两个 $\theta$ ）的大致图像，我们需要找到最低点时的 $\theta_j$ 的值。

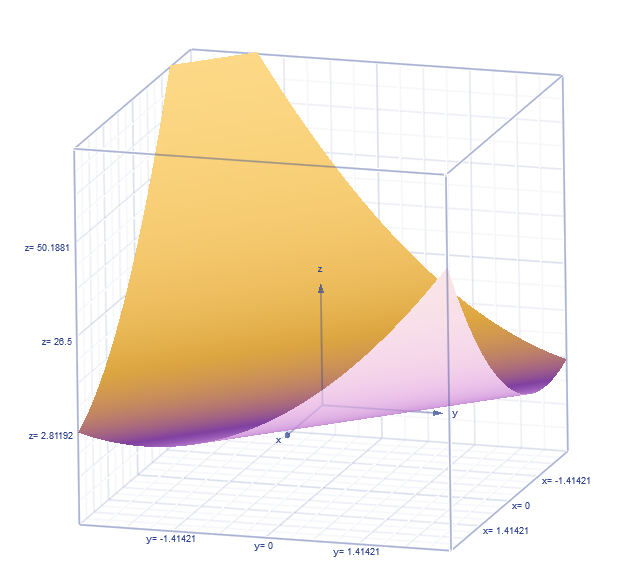
直接观察三维图像可能比较抽象，我们不妨先看二维，再拓展到三维。

在图中横截一条线如下图

注：曲线为函数图像；直线为对应点的切线（即 $J'(\theta_1)$ 项的值）

$y=\left(x-3\right)^{2}+1$
$y'_1=6x-26$
$y'_2=3.6x-13.04$
$y'_3=2x-6$
$y'_4=x-2.25$

数据如下表

$x$	$y$	$J'(\theta)$
6	10	6
4.8	4.24	3.6
4	2	2
3.5	1.25	1
3.2	1.04	0.4
3.1	1.01	0.2
3.05	1.0025	0.1
3	1	0

当 $k>0$ 时，说明 $\theta_1$ 位于 $\theta$ 的右侧，即要减去一个值

当 $k<0$ 时，说明 $\theta_1$ 位于 $\theta$ 的左侧，即要加上一个值

于是 $\theta_1=\theta_1-J'(\theta_1)\alpha$

实际上 $n$ 元线性回归（逻辑回归）是 $n+1$ 维的图像，我们可以类比理解。

实现

线性回归

//Linear Regression

#include <iostream>
#include <algorithm>
#include <ctime>
using namespace std;
int n,m;//n->data   m->w
double pre(double a[],double b[]){
    double h=0;
    for(int i=1;i<=m;i++){
        h=h+a[i]*b[i];
    }
    return h;
}
int main(){
    //clock_t start,end;
    double x[105][15],y[105],w[105],k=0.001,lam=0;
    w[0]=0;
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        x[i][0]=1;
        for(int j=1;j<=m;j++)
            cin>>x[i][j];
        cin>>y[i];
    }
   // start=clock();
    int iteration=200,q=0;
    double regular=lam/((double)n);
    //printf("%.3lf\n",regular);
    while(iteration--){
        for(int p=0;p<=m;p++){
            double s=0;
            for(int i=0;i<=n;i++){
                double predict=pre(x[i],w);
                double loss=predict-y[i];
                s=s+loss*x[i][p];
            }
            s=s/n;
           // printf("%.3lf\n",regular*w[p]);
            w[p]=w[p]-s*k-regular*w[p];
        }
        if(iteration%1==0){
            printf("Try %d:\t",++q);
            for(int i=0;i<=m;i++) printf("%.3lf  ",w[i]);
            printf("\n");
        }
    }
    printf("Result:  ");
    for(int i=0;i<=m;i++) printf("%.3lf  ",w[i]);
    printf("\n");
    //end=clock();
    //double uset=(double)(end-start)/CLOCKS_PER_SEC;
    //printf("Time: %.2lfs\n",uset);
    double xl[105];
    for(int i=1;i<=m;i++) cin>>xl[i];
    printf("%.0lf",pre(w,xl));
    return 0;
}

逻辑回归

//Logistic Regression

#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

int n,m;
double w[105];

double z(double xx[]){
	double h=0;
    for(int i=1;i<=m;i++){
        h=h+xx[i]*w[i];
    }
    return h;
}
double f(double zz){
    double tm1=exp(-zz);
    double tm2=1+tm1;
    double fin=1/tm2;
    return fin;
}
int main() {
    double x[20][105],y[200],aph=0.0001,lam=0;
    cin>>m>>n;
    for(int i=1;i<=m;i++){
        x[i][0]=1;
        for(int j=1;j<=n;j++) cin>>x[i][j];
        cin>>y[i];
    }//input
    int iter=2000;
    double regular=lam/((double)m);
	while(iter--){
        for(int j=0;j<=n;j++){
            double loss=0.00;
      		for(int i=0;i<=m;i++)
            	loss=loss+(f(z(x[i]))-y[i])*x[i][j];
            loss=loss/m;
            w[j]=w[j]-loss*aph-regular*w[j];
        }
        if(iter%100==0){
        	for(int k=0;k<=n;k++)
        		printf("%.3lf ",w[k]);
            printf("\n");
		}
    }
    printf("train over\n");
    for(int i=0;i<=n;i++) printf("%.3lf ",w[i]);
    printf("\n");
    return 0;
}

正规方程

定义

正规方程 (Normal Equation) ，是一个快速计算局部极值的方法。在数据量不大( $n<1000$ )左右时优于梯度下降算法（取决于个人机器性能限制）。

在知道表达式的情况下可以代替二分查找或三分查找。现在多用于s人工智能（机器学习）领域。

结合曾经的竞赛题目，这个技巧不太可能考到，但学习它还是需要的。

数学原理

不妨令

$X= \begin{bmatrix} 1&x_1^1&x_2^1&...&x_n^1\\ 1&x_1^2&x_2^2&...&x_n^1\\ &&...&\\ 1&x_1^m&x_2^m&...&x_n^m \end{bmatrix}$

$y= \begin{bmatrix} y^1\\y^2\\…\\y^m \end{bmatrix} ,\theta= \begin{bmatrix} \theta_1\\\theta_2\\…\\\theta_n \end{bmatrix}$

则预测函数为

$y=X\theta$

$\begin{aligned} \\&J(\theta)=(y-X\theta)^2\\ \end{aligned}$

$\begin{aligned} \frac{\partial J(\theta)} {\partial \theta} & = 2(y-X\theta)X^T \end{aligned}$

令上式为 $0$ 即得最小值

$\begin{aligned} 2(y-X\theta)X^T&=0\\ yX^T-X\theta X^T&=0\\ X^T\theta X&=yX^T\\ (X^TX)^{-1}X^TX\theta&=yX^T(X^TX)^{-1}\\ I\theta&=yX^T(X^TX)^{-1}\\ \theta &=(X^TX)^{-1}X^Ty \end{aligned}$

实现

$\text{C++}$ 可以使用矩阵计算库 Eigen 或手写矩阵计算

$\text{Python}$ 可以使用 Numpy 库或手写

此处使用 $\text{C++}$ 中的 Eigen 库实现

C++

// Normal Equation Methods
#include <iostream>
#include "eigen/Eigen/Eigen"
using namespace std;
using namespace Eigen;

Matrix<double,Dynamic,Dynamic> X;
Matrix<double,Dynamic,1> w;
Matrix<double,Dynamic,1> y;

int main() {
    int m,d;
    cin>>m>>d;
    X.resize(m,d+1);
    w.resize(d+1,1);
    y.resize(m,1);
    X.fill(1);
    for(int i=0;i<m;i++){//input data
        printf("\nX=\n");
        for(int j=1;j<=d;j++){
            int q;
            cin>>q;
            X(i,j)=q;
        }
        printf("y=");
        int q;
        cin>>q;
        y(i,0)=q;
    }
    w=(X*X.transpose()).inverse()*X.transpose()*y;//Normal Equation
    cout<<w;
    return 0;
}